Public Key
Introduction to what a public key is, how it is generated, and how it is represented.
Introduction to Public Keys
A public key is essentially a set of coordinate values on an elliptic curve, which can be calculated from a private key.
Elliptic Curve
An elliptic curve is a type of curve used in cryptographic systems. Point multiplication on the curve is used for encryption and decryption. A key characteristic of elliptic curves is that adding two points results in another point on the curve, allowing encryption through repeated addition.
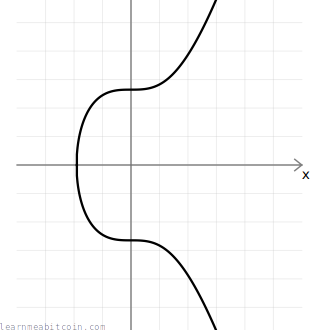
Definition of Elliptic Curve
An elliptic curve is usually represented by an equation of the form: For secp256k1, the specific form of the equation is: where (a = 0) and (b = 7).
The elliptic curve used by Bitcoin is a mathematical structure used for cryptography. Specifically, Bitcoin uses the elliptic curve secp256k1, defined over a finite field, commonly used in public key encryption.
How to Calculate a Public Key
Calculating a Public Key from a Private Key
- Choose the Base Point (G): The elliptic curve secp256k1 defines a base point ( G ), which is a fixed point with specific coordinates.
- Calculate the Public Key: Using the private key (( k )) and the base point (( G )), the public key (( K )) is calculated through point multiplication on the elliptic curve. This process is similar to scalar multiplication: Here, ( k ) is the private key, ( G ) is the base point, and ( K ) is the public key.
Point Multiplication
Point multiplication is not ordinary multiplication but is achieved through a series of point addition and point doubling on the elliptic curve. The brief steps are as follows:
-
Point Addition: If there are two points ( P = (x_1, y_1) ) and ( Q = (x_2, y_2) ), their sum ( R = (x_3, y_3) ) is calculated as follows:
- Calculate the slope ( m ):
- Calculate the coordinates of the new point:
-
Point Doubling: When ( P = Q ), the calculation is similar but with a different formula for the slope:
- Calculate the slope ( m ):
- Calculate the coordinates of the new point:
By repeatedly applying point addition and point doubling operations, the base point ( G ) can be transformed into the public key ( K ).
Security of Elliptic Curve Encryption
The security of elliptic curve encryption relies on the difficulty of the Elliptic Curve Discrete Logarithm Problem ( ECDLP). It is extremely difficult to deduce the private key ( k ) from the public key ( K ), ensuring the security of the encryption.