跳到主要内容

公钥

介绍什么是公钥，如何生成和表示公钥。

公钥简介​

公钥的本质是椭圆曲线上的一组坐标值，这个坐标可以通过私钥计算出来。

椭圆曲线​

椭圆曲线是密码学系统所使用的一种曲线。可以使用点乘运算来进行加密和解密。椭圆曲线的一个特点是，两个点相加后仍然在曲线上，这样就可以通过多次相加来实现加密。

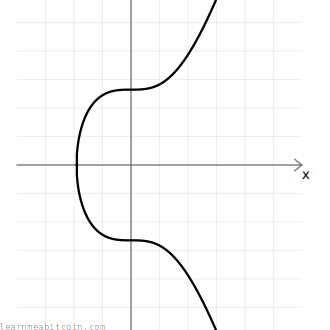
img.png

椭圆曲线的定义​

椭圆曲线通常表示为一个方程，形如： y2=x3+ax+by^2 = x^3 + ax + b 对于 secp256k1，方程的具体形式为： y2=x3+7y^2 = x^3 + 7 即 (a = 0)，(b = 7)。

比特币使用的椭圆曲线是一种用于密码学的数学结构。具体来说，比特币使用的是椭圆曲线 secp256k1，这是一种定义在有限域上的椭圆曲线，常用于公钥加密。

如何计算公钥​

从私钥计算公钥​

  1. 选择基点（G）：椭圆曲线 secp256k1 定义了一个基点 ( G )，这是一个固定的点，具有特定的坐标。
  2. 计算公钥：使用私钥（( k )）和基点（( G )），通过椭圆曲线上的点乘运算计算出公钥（( K )）。这个过程类似于标量乘法： K=k⋅GK = k \cdot G 这里，( k ) 是私钥，( G ) 是基点，( K ) 是公钥。

点乘运算​

点乘运算不是普通的乘法，而是通过一系列椭圆曲线上的点加法和倍加来实现的。简要步骤如下：

  1. 点加法（Point Addition）：如果有两个点 ( P = (x_1, y_1) ) 和 ( Q = (x_2, y_2) )，那么它们的和 ( R = (x_3, y_3) ) 的计算方式如下：

    • 计算斜率 ( m )： m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}
    • 计算新点的坐标： x3=m2−x1−x2x_3 = m^2 - x_1 - x_2 y3=m(x1−x3)−y1y_3 = m(x_1 - x_3) - y_1

  2. 点倍加（Point Doubling）：当 ( P = Q ) 时，计算方式类似，但斜率公式不同：

    • 计算斜率 ( m )： m=3x12+a2y1m = \frac{3x_1^2 + a}{2y_1}
    • 计算新点的坐标： x3=m2−2x1x_3 = m^2 - 2x_1 y3=m(x1−x3)−y1y_3 = m(x_1 - x_3) - y_1

通过不断应用点加法和点倍加操作，能将基点 ( G ) 变为公钥 ( K )。

椭圆曲线加密的安全性​

椭圆曲线加密的安全性依赖于椭圆曲线离散对数问题（ECDLP）的难度。即从公钥 ( K ) 推算私钥 ( k ) 是非常困难的，确保了加密的安全性。