Signature

Introduction to the signature system and why signatures ensure the security of the Bitcoin network.

Digital Signature

A signature is used to prove ownership of a set of public keys and authorize transactions. Bitcoin uses the Elliptic Curve Digital Signature Algorithm (ECDSA) to generate and verify signatures.

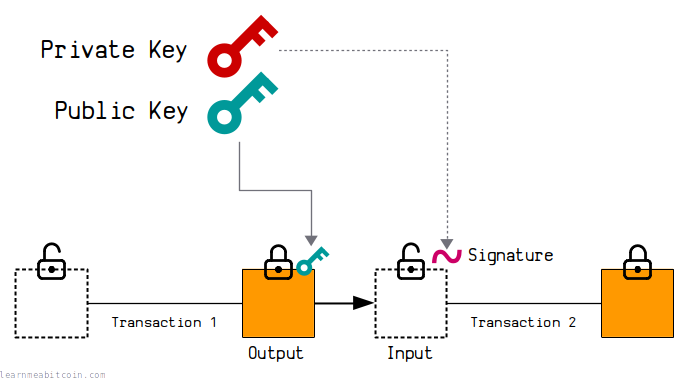
Bitcoin's Signature Mechanism

Bitcoin's signature mechanism is one of the core technologies ensuring the security and integrity of transactions. It is based on public key encryption algorithms, using digital signatures to verify the legitimacy of transactions and prevent tampering. Bitcoin uses the Elliptic Curve Digital Signature Algorithm (ECDSA) to create and verify signatures.

How to Create a Signature

The process of creating a Bitcoin transaction signature is as follows:

1. Generate Private Key: Each user generates a unique private key.
2. Generate Public Key: Use the elliptic curve algorithm (ECDSA) to generate the corresponding public key from the private key.
3. Create Transaction Hash: Hash the transaction data to generate a transaction hash (message hash). This includes the transaction's inputs, outputs, and other relevant data.
4. Generate Signature: Use the private key to sign the transaction hash, creating a digital signature.

Steps to Create a Signature

1. Select the Message: Choose the transaction data to be signed.
2. Calculate Hash: Hash the transaction data, usually using the SHA-256 algorithm.
3. Sign with Private Key: Use the private key to sign the hash value with ECDSA, generating the signature (r, s).

The mathematical process of generating a signature is as follows:

• Select a random number (k) (ensuring uniqueness and security).
• Compute (r = (k * G).x \mod n), where (G) is the base point of the elliptic curve, and (n) is the order of the curve.
• Compute (s = (z + r * d) / k \mod n), where (z) is the transaction hash, and (d) is the private key.

The final signature consists of (r, s).

Signature Encoding

Bitcoin signatures typically use the DER (Distinguished Encoding Rules) encoding format. DER is a binary encoding format of ASN.1, ensuring the standardization and consistency of signatures.

A DER-encoded signature consists of the following parts:

1. SEQUENCE: Indicates that the signature comprises multiple parts.
2. INTEGER r: The first integer part of the signature, r.
3. INTEGER s: The second integer part of the signature, s.

The steps for DER encoding are as follows:

1. Encode r and s: DER encode the two integer parts of the signature, r and s, separately.
2. Combine SEQUENCE: Combine the encoded results of r and s into a SEQUENCE.

An example of DER encoding is as follows:

• DER encoding of r: 02 <length_of_r> <r>
• DER encoding of s: 02 <length_of_s> <s>
• SEQUENCE encoding: 30 <length_of_sequence> <r_encoding> <s_encoding>

Signature Hash Type

The Signature Hash Type specifies the parts of the transaction to which the signature applies and influences the signature verification process. Common signature hash types in Bitcoin include:

1. SIGHASH_ALL (0x01): Signs the entire transaction, including all inputs and outputs. This is the most common signature hash type, ensuring the integrity of the transaction.
2. SIGHASH_NONE (0x02): Signs only the inputs, allowing outputs to be specified by other parts. Suitable for scenarios requiring flexible output adjustments.
3. SIGHASH_SINGLE (0x03): Signs a specific input and its corresponding output, allowing other outputs to change. Suitable for specifying a particular output.

For the Bitcoin Cash (BCH) network, signature hash types are extended with the SIGHASH_FORKID prefix to differentiate from the Bitcoin network. Refer to the table below for details:

Flag	Value including SIGHASH_FORKID	HEX / BINARY	Value excluding SIGHASH_FORKID	HEX / BINARY	Functional Meaning
SIGHASH_ALL	0x41	0100 0001	0x01	0000 0001	Sign all inputs and outputs
SIGHASH_NONE	0x42	0100 0010	0x02	0000 0010	Sign all inputs and no output
SIGHASH_SINGLE	0x43	0100 0011	0x03	0000 0011	Sign all inputs and the output with the same index
SIGHASH_ALL	ANYONECANPAY	0xC1	1100 0001	0x81	1000 0001
SIGHASH_NONE	ANYONECANPAY	0xC2	1100 0010	0x82	1000 0010
SIGHASH_SINGLE	ANYONECANPAY	0xC3	1100 0011	0x83	1000 0011

Example of the Signature Process

Suppose there is a Bitcoin transaction that needs to be signed, and the SIGHASH_ALL type is chosen. The steps for signing are as follows:

1. Generate Transaction Hash: Hash the transaction data.
2. Select Signature Hash Type: Add the SIGHASH_ALL flag.
3. Generate Signature: Use the private key to sign the transaction hash, resulting in a DER-encoded signature.
4. Append Signature Hash Type: Append the SIGHASH_ALL flag to the signature.

Summary

Bitcoin's signature mechanism ensures the security and integrity of transactions through the ECDSA algorithm. The process of creating a signature involves generating a private key, generating a public key, calculating the transaction hash, and generating the signature. DER encoding standardizes the representation of signatures, ensuring their consistency. Different Signature Hash Types provide flexible signature verification methods, catering to various transaction needs. Understanding Bitcoin's signature mechanism helps to deeply understand the security and technical details of Bitcoin transactions.